Технология решения трехмерных задач гравиметрии.

Введение.

Технология, по нашему представлению, должна включать в себя технические средства, программное обеспечение и методику их использования для решения определенных задач.

В предлагаемой технологии в качестве технических средств предлагается использовать современные персональные компьютеры(PC) с большими объемами памяти и с большим быстродействием.

Наиболее важными и трудоемкими в гравиметрии являются обратные задачи гравиметрии. В двухмерном варианте они часто решаются методом подбора. Но в больших двухмерных и, тем более, трехмерных задачах таким способом обратные задачи решать трудно, а иногда и невозможно. Известно, что обратные задачи гравиметрии могут быть сведены к решению систем алгебраических уравнений (линейных или нелинейных). При решении этих систем возникает ряд трудностей, о которых довольно много написано статей и довольно детально об этом сказано в работах В.Н. Страхова. О технических трудностях написано в его работе "Что делать"[7]. В данном докладе мы не будем обсуждать эту сторону вопроса, а перейдем к обсуждению конкретных технических решений, преодолевающих многие трудности.

В качестве метода решения систем алгебраических уравнений выбран итерационно стохастический (адаптивный) метод [4,5,6,7].Его особенностью является то, что он не накапливает ошибок и позволяет решать системы с большим числом(m) уравнений и большим числом(n) неизвестных. Причем могут быть любые соотношения m и n (т.е. может быть m=n, m>n и m

Модель среды, постановка задачи и метод решения обратных задач.

Для решения задач гравиметрии принята трехмерная (в частном случае двухмерная) слоистая модель среды с криволинейными границами раздела слоев. Каждый слой аппроксимируется элементарными параллелепипедами (блоками). По осям X и Y разбиение на блоки идет с заданными шагами, а вертикальные размеры блоков определяются положением границ. В пределах элементарного блока плотность породы считается постоянной.

На этой модели рассматриваются три задачи: прямая, обратная и контактная.

Прямая задача решается путем суммирования гравиметрического эффекта от каждого блока модели. Для расчета влияния блока используются формулы, известные из работ [1,8]. Решение обратной задачи сводится к решению системы линейных уравнений. Система, описывающая контактную задачу, нелинейна. Ее коэффициенты сами зависят от положения искомых границ. Обе эти системы решаются итерационно стохастическим (адаптивным) методом [4,5,6,7]. Причем, в контактной задаче коэффициенты системы уточняются после каждой итерации.

Применяемый адаптивный метод обладает следующими основными особенностями:

1. использует начальные приближения неизвестных плотностей (или границ);
2. учитывает их среднеквадратические ошибки (СКО), а также СКО значений гравитационного поля;
3. не накапливает ошибок округления, что позволяет решать системы с большим числом уравнений и неизвестных;
4. позволяет находить решение ближайшее к априорно заданному в том случае, когда задача имеет множество решений.

Результатом решения обратной гравиметрической задачи является блочная модель с полностью определенными плотностями, границами и подобранным (модельным) полем. На этой модели может быть приближенно решена дополнительная задача по получению слоисто-однородной модели с числом слоев вдвое большим, чем в исходной. Для этого каждый слой расчленяется на два подслоя с предположением, что плотности в подслоях постоянны. Первоначальное значение этих плотностей выбирается автоматически: верхнему подслою присваивается минимальное, а нижнему - максимальное из всех блоков данного слоя значение плотности. Алгоритм вычисляет положение новой границы внутри каждого блока таким образом, чтобы общая масса двух новых блоков была равна массе включающего их блока. Имеется возможность вручную и визуально подбирать значение плотностей подслоев и, соответственно, положение новых границ раздела. Полученная таким способом новая модель может служить начальным приближением в контактной задаче для последующего уточнения границ.

И, наконец, в качестве еще одного дополнительного результата, вычисляются средние скорости, нулевые времена пробега волн, отраженных от каждой границы, и статические поправки за пункт приема отраженных волн. Эти возможности используются для совместной интерпретации данных сейсморазведки и гравиметрии.

Краткая характеристика пакета.

Ниже приведены основные паспортные данные пакета:

Примечание: число слоев и блоков в слое ограничено возможностями компьютера. Например, при создании модели 1000x1000x1000 компьютеру требуется 43 Гб памяти только для хранения в ней модели. Правда, для решения требуется еще не более 8 Мб памяти.

Основные технические возможности.

В пакете предусмотрена возможность выбора данных из таблиц текстового формата и включение их в нужный массив(импорт).

Предусмотрены текстовый и графический редакторы массивов (границ, плотностей).

Для оперативного анализа результаты визуализируются в объемном(3D) виде и на плоскости в виде карт параметров с цветным заполнением с изолиниями или без них. Для получения изображений в других пакетах, предусмотрен вывод (экспорт) данных в виде текстовых таблиц.

Для иллюстрации некоторых возможностей пакета ниже приведены сравнительно простые варианты решения обратных задач по реальным данным.

Пример решения обратной задачи.

Для решения были даны значения аномалии Буге с плотностью в верхнем слое 2.67 г/см3.

Точки наблюдения расположены на 100-х профилях с шагом между ними 765.25 м и числом точек на профилях 84 с шагом 763.25 м. В пакете сделана процедура импорта, которая при импорте grid-файла определяет шаг между профилями и шаг между точками.

Для изучения возможностей пакета при решении обратной задачи в однослойной модели, проведем серию экспериментов, изменяя границу нижнего слоя. Результаты эксперимента приведены в табл.1.

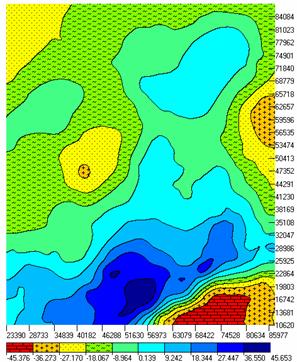
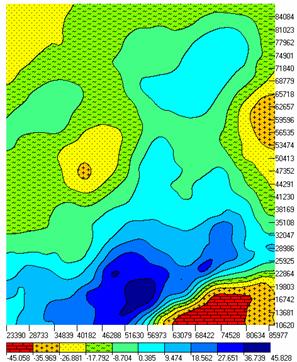
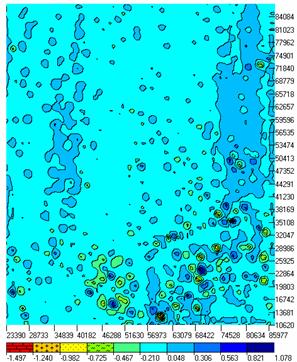
Время счета каждого эксперимента составляет 41 минуту при процессоре 1000 мегагерц.

Анализируя таблицу, видим, что с увеличением абсолютной отметки подошвы увеличиваются минимальные (от 1.169 до 2.41) значения плотностей и уменьшаются максимальные (от 3.6 до 2.96). Несмотря на значительное изменение подошвы (от 1000 до 10000 м) и при наличии сильных аномалий на краях в результатах нет видимых искажений, связанных с краевыми эффектами. По результатам анализа в качестве исходного для дальнейшей обработки примем вариант, в котором Z=5000 м. Для этого варианта приведем сопоставление исходного поля и подобранного при решении обратной задачи. Как видно (рис.1), исходное и подобранное поля практически не отличаются.

Разности полей приведены в кадре В. В разности отличия в основном локального характера.

Для иллюстрации возможностей пакета на рис.2 показаны гравитационное поле и трехмерная модель среды.

Авторы выражают благодарность руководству Гравиметрической экспедиции №3 за поддержку в создании технологии.

Рисунки.

Исходное	Модельное
Разность

Литература.

1. Алексидзе М.А. Приближенные методы решения прямых и обратных задач гравиметрии.- М.: Наука, 1987.- 336с.
2. Гравиразведка. Справочник геофизика.- M.: Недра, 1980.- 616с.
3. Кочнев В.А. Адаптивные методы интерпретации сейсмических данных.- Новосибирск: Наука, 1988.- 152с.
4. Кочнев В.А. Адаптивные методы решения обратных задач геофизики. - ВЦ СО РАН, Красноярск, учебное пособие, 1993.
5. Кочнев В.А., Хвостенко В.И. Адаптивный метод решения обратных задач гравиметрии. - Геология и геофизика, №7, 1996, с.120-129.
6. Кочнев В.А. Путь осознания возможностей математических моделей и алгебраических уравнений в геофизике. - Геофизика, №5, 2001, с. 20-23.
7. Страхов В.Н. 1998. Что делать? (О развитии гравиметрии и магнитометрии в России в начале XXI века). РАН, объединенный институт физики земли им. В.Ю. Шлитта. - М. - 24с.
8. Ломтадзе В.В. Новые возможности способа эквивалентных призм при интерпретации аномалий силы тяжести./ Прикладная геофизика #113.-М.: Недра, 1985.- с.85-92.